Кодировки UTF-8, UTF-16, UTF-32. История кодировок.

Компьютер, это машина работающая с числами. Человек работает с числами, текстом, формулами, изображениями, которые преобразуются в текст и так далее. Каким образом мы адаптировались друг к другу? Как компьютер понимает букву, слово, предложение?

Любой текстовый символ можно обозначить каким-то конкретным числом и таким образом хранить его в памяти. Так оно и происходит. Когда компьютер читает код символа из памяти, он видит, что этот код соответствует буквы А и выводит букву А на экран. Чтобы это число отображалось на экране, именно таким символом, все компьютеры на планете должны использовать один и тот же стандарт – некие таблицы, в которых указано, какому символу какое число соответствует.

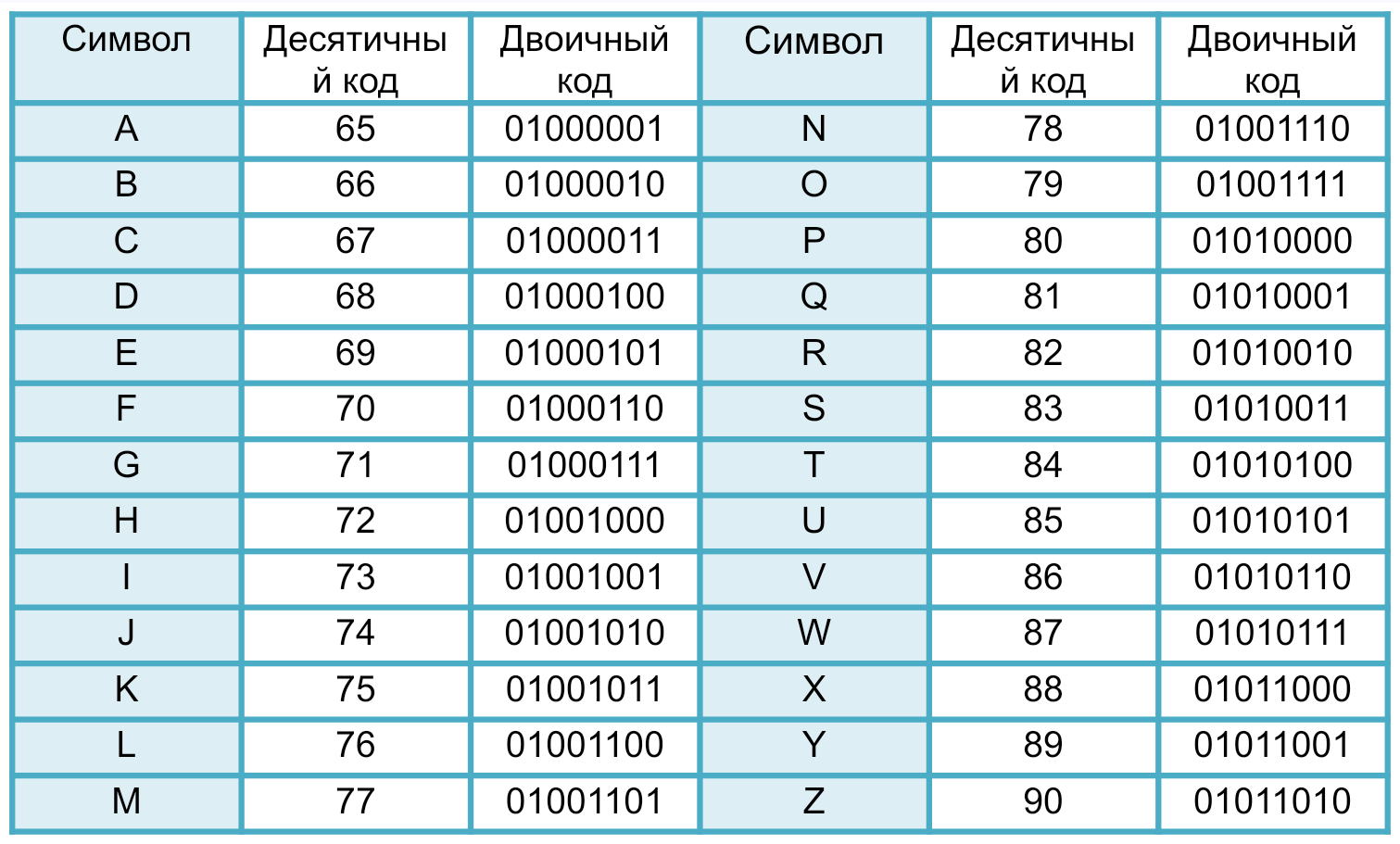
Таблица символ/десятичный код/двоичный код.

Первый ноль слева не входит в код буквы. Его добавляют, чтобы создать байт. В памяти можно выделять только байты, а не отдельные биты.

Звучит просто, но на деле развитие этих стандартов сопровождалось чередой глобальных проблем, которые не были заранее предусмотрены. Работа со строками это одна из самых важных тем, во всем программировании, потому что строки это основной вид информации, с которым работает человек.

Далее, рассмотрим развитие стандартов, кодировок и во что все это вылилось на текущий момент. Итак, каждый символ в компьютере представляется в виде целого числа. Это число называется кодом символа. Для того, чтобы мы могли использовать текстовую информацию на разных компьютерах, они должны поддерживать одни и те же коды символов. Иначе, один и тот же символ будет отображаться по разному на разных компьютерах, и обмен информацией станет невозможным.

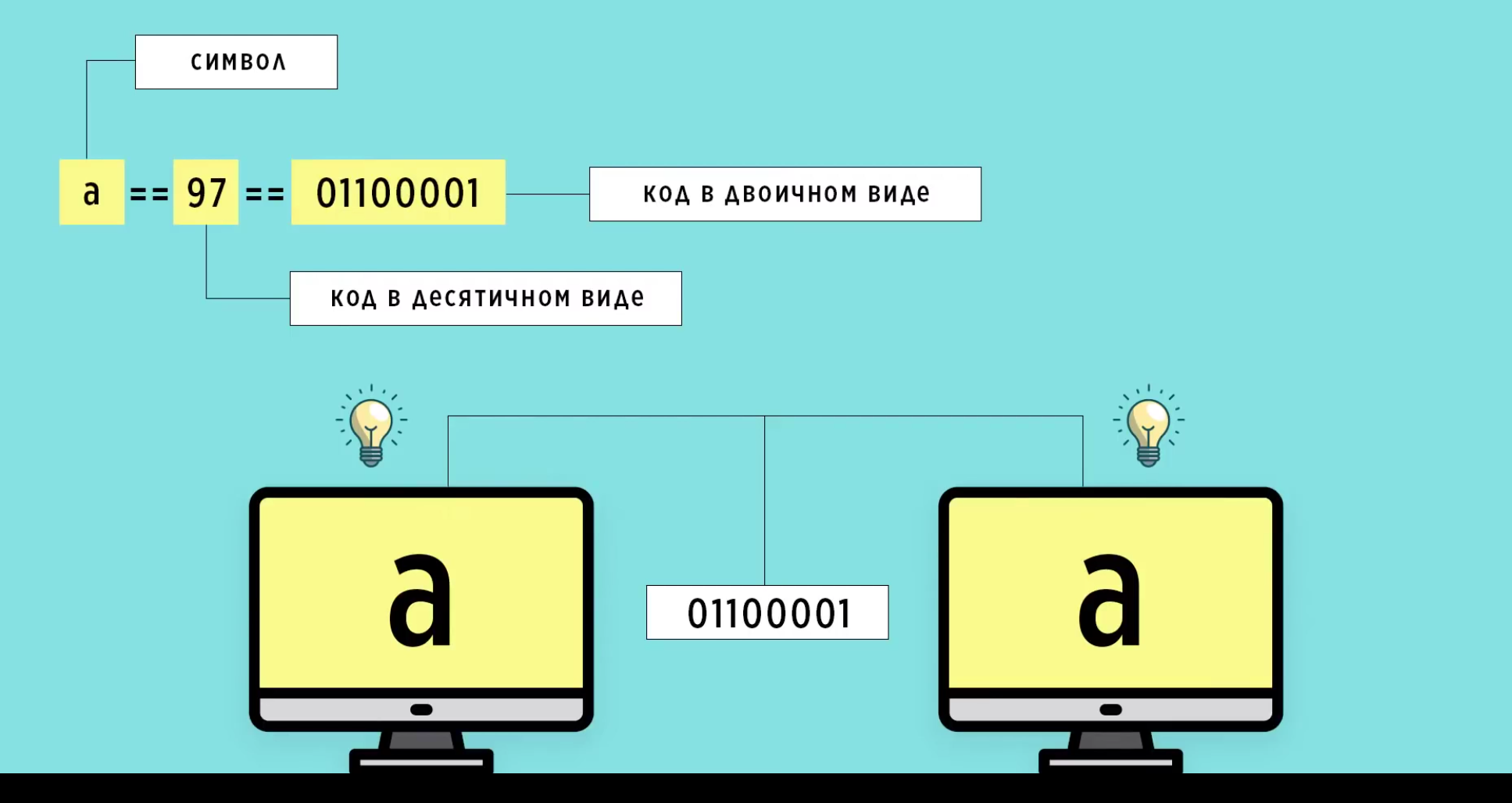
2 компьютера, одинаковый код в двоичном виде

Как перевести число в двоичный код?

Чтобы преобразовать число 97 в двоичный код, нужно разделить его на 2 и записать результаты деления. Вот шаги:
⦁ 97 : 2 = 48 (остаток 1).
⦁ 48 : 2 = 24 (остаток 0).
⦁ 24 : 2 = 12 (остаток 0).
⦁ 12 : 2 = 6 (остаток 0).
⦁ 6 : 2 = 3 (остаток 0).
⦁ 3 : 2 = 1 (остаток 1).
⦁ 1 : 2 = 0 (остаток 1).
Таким образом, двоичный код числа 97 равен 1100001. Это остаток снизу вверх. Первый слева ноль на фото, это пустой бит. О нём будет сказано позже.

Итак, чтобы буква а на всех компьютерах отображалась одинаково, коды символов нужно стандартизировать. Поэтому, были разработаны стандарты. Но, компьютерные технологии развивались преимущественно в США, и входе экспериментов там был создан стандарт, подходящий для английского языка. Стандарт получил название ASCII.

Примечание.
ASCII расшифровывается: "American standard code for information interchange". Переводится: "Американский стандартный код для обмена информацией". Принят в 1963 году Американской ассоциацией стандартов как основной способ представления текстовых данных в ЭВМ.

В ходе разработки стандарта не учитывались потребности в символах других языков, поэтому на каждый символ ASCII было выделено всего 7 бит.

Что такое 1 бит?

Бит – это самая маленькая единица информации, принимающая одно из двух значений: 0 или 1. В вычислительной технике "0" и "1" обычно создаются разными уровнями напряжения или тока. Например, в транзисторных схемах значение "0" представляется напряжением в диапазоне от 0 до +0,8 вольт, а значение "1" – напряжением в диапазоне от +2,4 до +5,0 вольт. Другими словами, если на выходе транзистора нет напряжения, то это ноль. Если есть, то это единица. Выход первого транзистора является входом второго и так далее. Вот почему иногда говорят, что 1 бит информации – символ или сигнал, который может принимать два значения: включено или выключено, да или нет, высокий или низкий, заряженный или незаряженный. В двоичной системе счисления это 1 или 0.

О самом понятии.

Система счисления – это способ записи (представления) чисел. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления у числа указывается нижний индекса. Таким образом, 503 = 503₁₀ . С помощью индекса мы понимаем в какой системе записано число.

Зачем использовать двоичную систему счисления?

Ведь можно создать устройство с 10 устойчивыми состояниями. На выходе будет 1 вольт напряжения, 2 вольта, ….. 9 вольт, 10 вольт. Ведь создали, например, обычный домашний телефон. У него 10 цифр и цифрам соответствуют 10 устойчивых состояний. Тогда можно использовать десятичную систему счисления, привычную нам. Почему же сложилось так, что компьютеры используют двоичную систему?

В ранние годы развития компьютеров в качестве основы для вычислений рассматривались различные системы счисления. Однако двоичная система была выбрана по следующим причинам:
⦁ Технологические ограничения.
Ранние компьютеры использовали электромеханические реле и вакуумные лампы, которые имели только два устойчивых состояния.
⦁ Стоимость.
Реализация устройств с 10 устойчивыми состояниями была бы более сложной и дорогой.
⦁ Производительность.
Двоичная арифметика оказалась более быстрой и эффективной.
⦁ Простота отладки.
Ошибки в двоичном коде было легче обнаруживать и устранять.

Это, как говорится, "на пальцах" для понимания. Более общими словами, о преимуществах двоичной системы счисления:
⦁ Простота аппаратной реализации.
Логические элементы в компьютерах имеют только два устойчивых состояния (например, включено или выключено), что делает двоичную систему естественным выбором для вычислений. Логические схемы намного проще в реализации.
⦁ Эффективность.
Двоичная система требует всего двух символов (0 и 1), что упрощает хранение и обработку информации.
⦁ Наглядность.
Двоичные числа легче представлять и понимать, чем числа в других системах счисления.
⦁ Надежность.
С двумя состояниями вероятность ошибки меньше, чем в системах с большим количеством состояний. Компьютерные вычисления, как правило, очень точны и не содержат ошибок.
⦁ Достигается универсальность.
Двоичная система теперь является основой всех современных цифровых компьютеров и электронных устройств.

Продолжаем, в 7 бит помещаются числа от 0 по 127, и таким образом всего можно было закодировать 128 символ. 128 потому, что число 0 тоже входит:
⦁ Для десятичного числа 0 двоичный код равен 0.
0 ÷ 2 = 0 (остаток 0)
⦁ Для десятичного числа 127 двоичный код равен 1111111.
127 : 2 = 63 (остаток 1)
63 : 2 = 31 (остаток 1)
31 : 2 = 15 (остаток 1)
15 : 2 = 7 (остаток 1)
7 : 2 = 3 (остаток 1)
3 : 2 = 1 (остаток 1)
1 : 2 = 0 (остаток 1)

1 байт.

Минимальная ячейка памяти, которую можно отрисовать, составляет 8 бит или это 1 байт. Поэтому, для хранения каждого символа ASCII используется один байт, который способен хранить в себе 256 значений.

Откуда это число – 256 значений?

Десятичное число 255. Двоичное: 11111111, то есть все восемь ячеек заняты единицами. 256 - ое значение, это ноль.

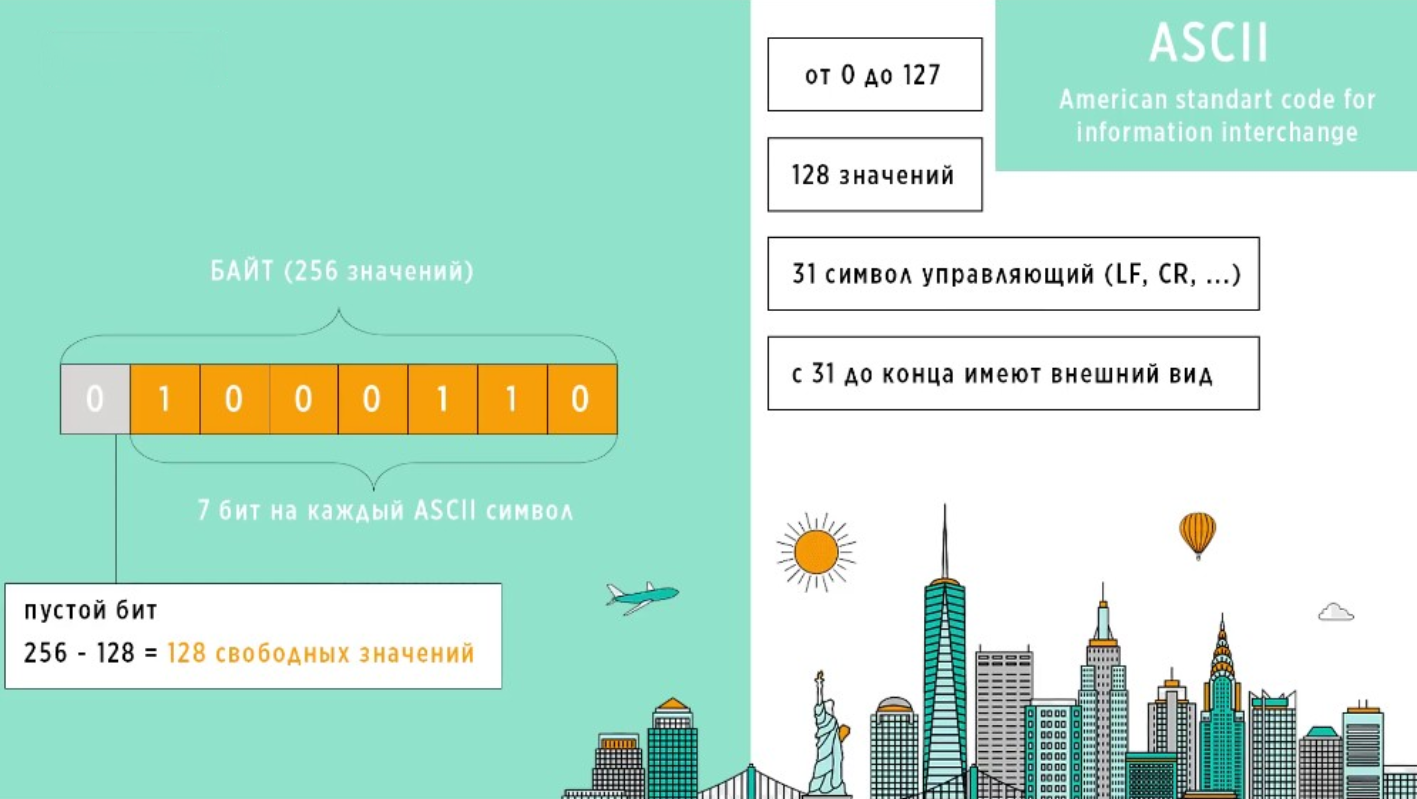
Кодировка ASCII, 8 клеточек показывают 8 бит, двоичная система

Так как символы 7 битные, то 1 бит в этой ячейке всегда будет оставаться в пустым. Таким образом, остается место для 128 значений, которые никем не используются. В этом стандарте первые 31 символ, являются управляющими, они не отображаются на экране, а используются для выполнения каких-либо действий. Например, это символы перевода строки, возврата каретки и так далее. Все последующие символы имеют внешний вид и отображаются на экране.

Пока программное обеспечение преимущественно выпускалось для англоязычной аудитории, все было хорошо, но время шло и компьютеры стали распространяться по всему миру. Стало необходимостью выпускать программное обеспечение не только для англоязычной аудитории, но и для остальных пользователей, которые по- английски не говорят.

Во многих европейских странах есть буквы, которых нет английском алфавите, а в таких языках, как русский, китайский, арабский и так далее, алфавит вообще кардинально отличается. Разумеется, что используя только 7 бит, невозможно охватить все необходимые символы, включая десятки тысяч иероглифов разных языков. Нужно было как-то решить проблему с нехваткой символов, и так как оставалось еще 128 мест внутри байта, стандарт ASCII решили расширить введя кодовые страницы.

Кодовая страница – это набор из 256 символов для конкретного языка. Первый 128 символов полностью совпадали с символами ASCII. Остальные 128 символов в разных кодовых страницах были разные в зависимости от языка, для которого предназначалась эта страница. В каждой стране начали добавлять символы своего алфавита, в свободный 128 мест. Причем каждый добавлял их как хотел. Например, в одной той же стране могли сделать сразу по несколько разных кодовых страниц с символами в разном порядке. Не было никакой упорядоченности, и это выливалось в то, что если два разных компьютера использовали две разные кодовые страницы, то текст, переданный с одного устройства, на втором был просто не читаем.

В любом случае кодовые страницы имея в своем распоряжении всего 256 символов, не могли охватить все возможные языки. Плюс проблему усугубилась, когда появился интернет. Люди начали обмениваться информацией, используя разные кодовые страницы, и отсутствие какой-либо мировой стандартизации привело всё к хаосу. Параллельно с развитием компьютеров стали развиваться операционные системы. На первый план вышла операционная система Windows. Она взяла за основу стандарт ASCII, расширила его своими символами и назвала ANSI. Далее на основе ANSI начали создаваться кодовые страницы, под названием Windows-125x, где x – это номер страны. Например, для кириллицы это было Windows-1251.

Вскоре Windows точно так же распространилась по всему миру, дойдя до Азии, где кодовыми страницами проблему было не решить. 256 значений в байте против тысячи иероглифов в алфавитах. Windows попытались придумать новый способ кодирования, где для хранения одних символов использовался бы один байд, а для других два.

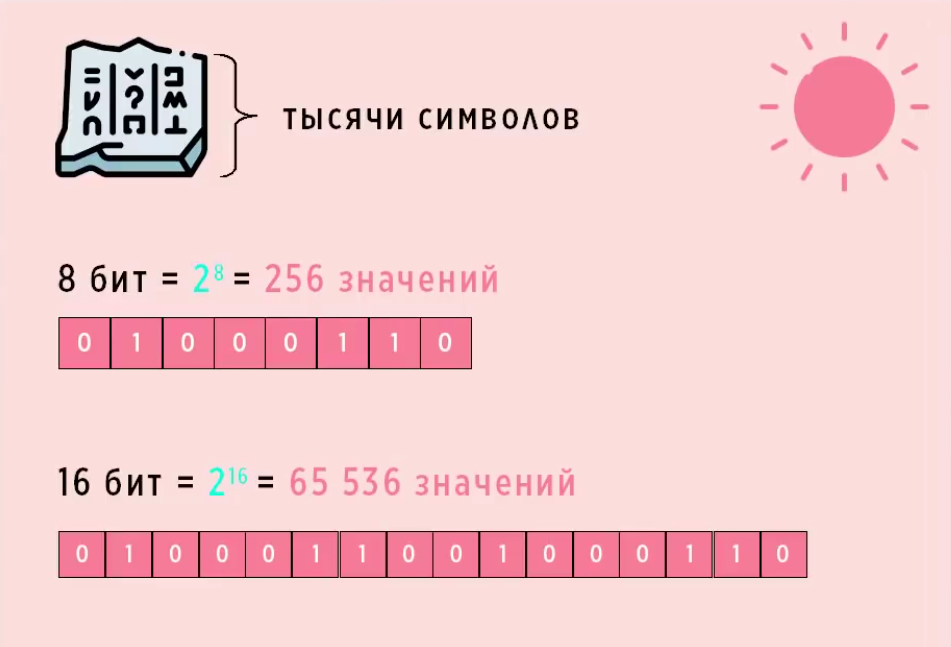
Если кто не помнит как считать 2⁸.

Перемножаем восемь двоек.
2⁸ = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256
Для 2₁₆ перемножаем шестнадцать двоек. Получим 65536.

Почему перемножать двойки?

Для понимания рассмотрим только 2 бита, то есть только 2 ячейки. Каждая ячейка может принимать два значения. По аналогии можем записать:
2² = 2 x 2 = 4 варианта двоичного кода должны получить.

Две клеточки, в каждой 0 — Проверяем. 1 вариант:

Две клеточки, в левой 0, в правой 1 — 2 вариант:

Две клеточки, в левой 1, в правой 0 — 3 вариант:

Продолжаем об истории создания кодировок.

Использование двух байтов для хранения символов, решило отдельно взятую проблему Microsoft с кодированием, но это не решало общую проблему стандартизации. Каждый продолжал пользоваться тем, чем хотел и пересылая по интернету текст в одной кодировке, он не мог корректно отображаться в другой кодировке на компьютере получатель. Нужно было придумать единый стандарт кодирования символов для всех языков мира. Таким образом, появился международный стандарт Unicode, призванный заменить собой ASCII.

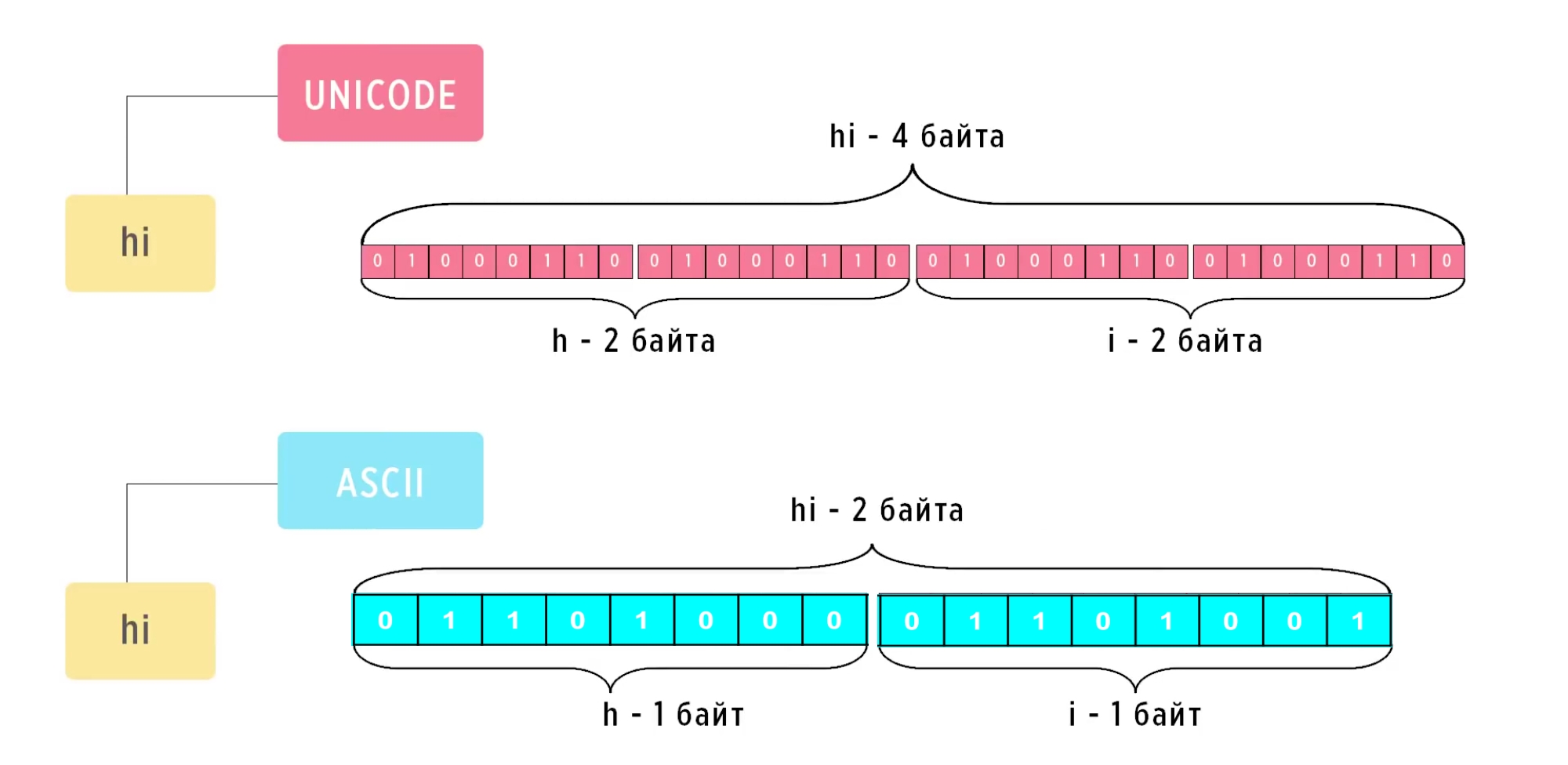
Его особенность заключалась в том, что если в стандарте ASCII на каждый символ выделялось 7 бит и максимальное количество символов составляло 128, то для Unicode не было никаких ограничений на количество символов. Каждый его символ представлялся минимум двумя байтами и в первую версию Unicode все необходимые символы как раз умещались в эти два байта, то есть их размер не превышал 65536 кодов.

Каждому символу по-прежнему соответствовал определенный числовой код, но при этом для записи было принято использовать такой формат – U плюс код символа.

Второй важный момент был в том, что первые 128 символов полностью совпадали с ASCII.

Со временем появлялись новые символы, иконки, смайлики и Юникод стал расширяться, что продолжается по сей день. На текущий момент версия 15.1.0 стандарта определяет 149 813 символов, используемых в различных обычных, литературных, академических и технических контекстах. Ознакомится с таблицами Юникода версии 15.0, а также скачать таблицы в виде документа PDF можно Здесь1 .

Юникод решил вопрос с кодированием большого количества символов и казалась трудности на этом должны были закончиться. Однако, появление Юникода привело к другим проблемам, которые также предстояло решать. Первая заключалась в том, что любые символы в Юникоде занимали минимум 16 бит. Это воспринималось как расточительство памяти в англоязычных странах, в которых можно было использовать ASCII. Зачем использовать 16 бит для символов английского алфавита, когда можно использовать семи битный код ASCII и экономить память в два раза? По этой причине многие продолжали пользоваться ASCII, игнорирую Юникод.

Другая проблема была связана с разным порядком расположения байт в памяти компьютера. В том случае, если число не может быть представлено одним байтом, имеет значение, в каком порядке байты записываются в памяти компьютера или передаются по линиям связи. Следует учитывать этот порядок записи. Байты могут располагаться в прямой и обратной последовательности, так называемый big endian и little endian. В настоящее время распространены эти 2 порядка. Порядок big-endian предполагает расположение байтов от старшего к младшему. Порядок little-endian предполагает расположение байтов от младшего к старшему.

Что это такое и как это работает?

Раньше такой проблема не было, потому что при ASCII использовался один байт и было не важно в каком порядке они передавались. В Юникоде каждый символ состоит из двух байт. Какой из этих байтов является началом, а какой концом попробуй разбери.

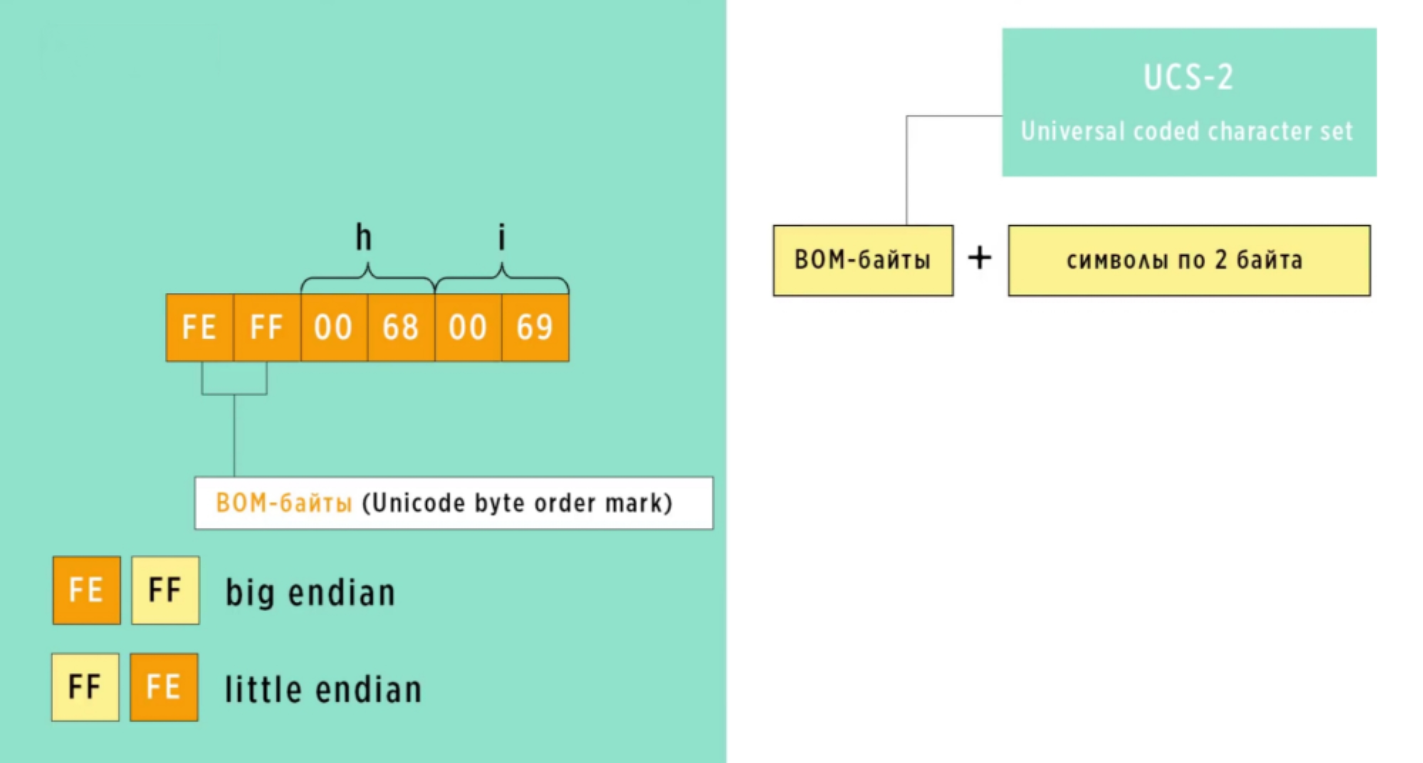
Например, строка hi в Юникоде:
⦁ Символ h имеет код 0068. Можно посмотреть в таблице Unicode по ссылке указанной выше, найдя букву h. При big endian код будет храниться в точно таком же порядке.
⦁ При little endian байты в двухбайтовом коде для буквы h поменяются местами и получится 6800.
Для буквы i будет так же.

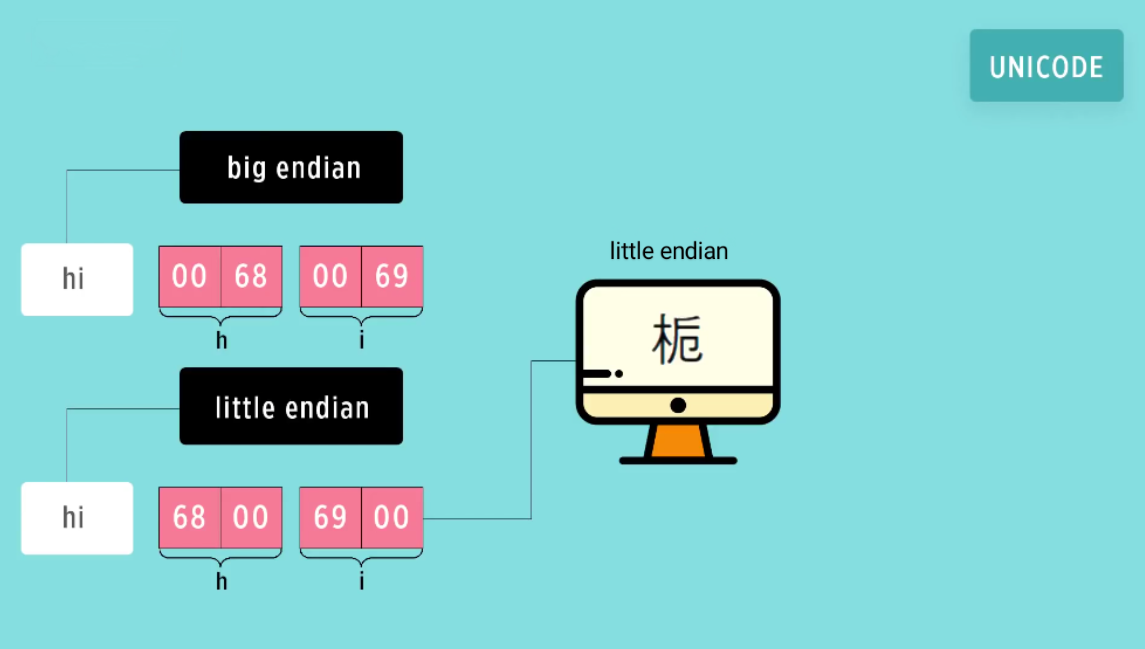
В итоге, при чтении этого символа из памяти, такой код в Юникоде будет выглядеть не как буква h, а как такой вот иероглиф. Его можно посмотреть в таблице Unicode по коду иероглифа 6800, если скачать таблицу.

Чтобы решить проблему с порядком хранения строк в памяти, появляются кодировки. Можно сказать, что кодировка – это правило, описывающие хранения символов Unicode в памяти. Одна из первых кодировок получила название UCS-2 (Universal coded character set). Эта кодировка хранила все символы, используя фиксированную длину к два байта, отсюда цифра 2 в названии. В этой кодировке проблему с порядком хранения байтов решили следующим образом: перед отправкой или сохранением файла, в самое начало добавлялось двухбайтовое число, которое получило название бом-байты или BOM-байты (Unicode byte order mark). Если использовался big endian, то эти байты шли прямой последовательности. Если little endian, то они менялись местами. Получавший компьютер, считывал эти первые два байта и понимал, в какой последовательности расположена строка. В результате такого решения Юникод-строка стала занимать еще больше памяти, чем было.

UTF-8.

Чтобы угодить всем, нужна была более универсальная кодировка, которая могла бы решать проблему как с хранением порядка символов, так и с экономией места. Такой кодировкой стала UTF-8 (Unicode transformaton format / Формат преобразования Юникода). Именно она в последствии стала доминирующей кодировкой в интернете. Решение заключалось в том, чтобы сделать коды символов нефиксированной, а переменной длинны от одного до четырех байт. Восьмерка в названии стоит как раз потому, что минимальная длинна, в которой может быть представлен символ, составляет 8 бит. Важный момент здесь в том, что первые 128 символов Юникода полностью совпадают первыми 128 символами ASCII, поэтому в кодировке UTF-8 эти первые 128 символов хранятся в памяти, используя только один байт. То, чего все так долго ждали. Остальные символы, от 128 и дальше, занимают память от двух до четырех байт.

Чтобы понять, каким образом решилась проблема с BOM-байтами, посмотрим, как UTF-8 кодирует символы разной длинны. Существует четыре маски (шаблона) для кодов, разной длинны. Если первым в символе идёт ноль, кодировка понимает, что это один восьмибитный символ. Двух-, трёх- и четырёхбайтные символы всегда начинаются с единицы.

Итак, в UTF-8 каждый символ кодируется разным количеством байтов – всё зависит от того, какой длины исходное число:
⦁ До 7 бит – выделяется один байт.
⦁ 8-11 бит – выделяется два байта.
⦁ 12-16 бит – тут уже три байта.
⦁ 17-21 бит – для кодирования нужно четыре байта.

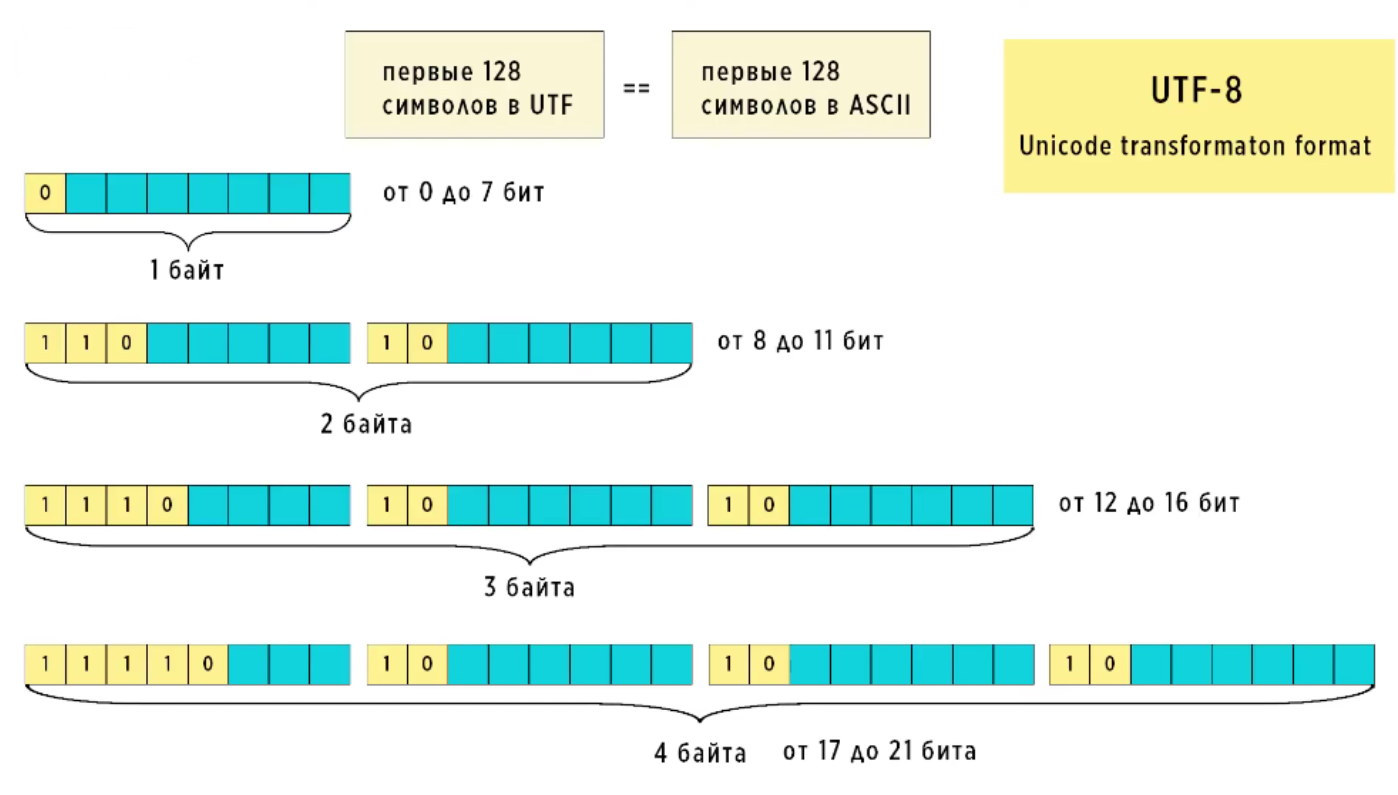
Длина первых 128 кодов помещается в диапазон от нуля до 7 бит включительно, поэтому хранится они будут согласно маски и длинны. В начале байта ставится 0, далее записывается код символа и в таком виде он сохраняется памяти. Далее все по аналогии. Для кода соответствующей длинны будет использоваться соответствующая маска. В самом начале байтов ставятся специальные метки и в таком виде все это сохраняется в памяти. Эти метки определяют, сколько байт нужно прочитать из памяти. Если в начале байта стоит последовательность 110, значит нужно прочитать 2 байта. Если 1110, значит 3 байта и так далее. По этим же самым меткам можно было определить, где находится начало символа. Каждый байт продолжения начинается с 10.

Благодаря специальным меткам в этой кодировке можно было не использовать BOM-байты. Так называемый UTF-8 без BOM, то есть в начале символа всегда будет одно из этих значений:

Если в компьютере используется big endian, то он увидит одно из этих чисел. Например 1110 и поймёт, что это начало символа, который состоит из трех байт. Читаем 3 байта и идем дальше. Если используется little endian, то первый байт будет начинаться с 10. В таком случае компьютер поймёт, что надо идти назад до тех пор, пока не будет найдена 1 из 4 последовательностей, с которой символ должен начинаться.

Рассмотрим пример для символа П.

В Юникоде код этого символа имеет вид 041F в шестнадцатеричной системе счисления.

Примечание.
Шестнадцатеричная – считают по 16, а не по 10, чтобы получился следующий разряд числа. Если речь о таблице, в которой представлен какой-то символ, то это таблица с 16 клетками по горизонтали и 16 клетками по вертикали. В десятичной системе для записи числа используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В шестнадцатеричной системе для записи числа используются цифры и буквы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Смотри по ссылке выше на таблицу Юникода, страница 9 документа PDF для кириллицы.

Разряд числа – это место (позиция) цифры в записи данного числа. Например, в трёхзначном числе 873 цифра 3 обозначает количество единиц нулевого разряда, 7 – первого, 8 – второго. В десятичной системе счисления каждая позиция представляет степень числа 10.

В числе 783:
⦁ Цифра 3 находится на самом правом месте, и ее разряд называется единицами.
Она представляет 3 * 10⁰ = 3.
⦁ Цифра 8 находится на втором месте справа и ее разряд называется десятками.
Она представляет 8 * 10¹ = 80.
⦁ Цифра 7 находится на третьем месте справа и ее разряд называется сотнями.
Она представляет 7 * 10² = 700.

Таким образом, цифра 3 находится на нулевом разряде, так как она стоит в позиции единиц, которая соответствует 10⁰. Важно отметить, что в некоторых источниках разряды нумеруют с 1, начиная с единиц. В этом случае разряд цифры 3 будет считаться первым.

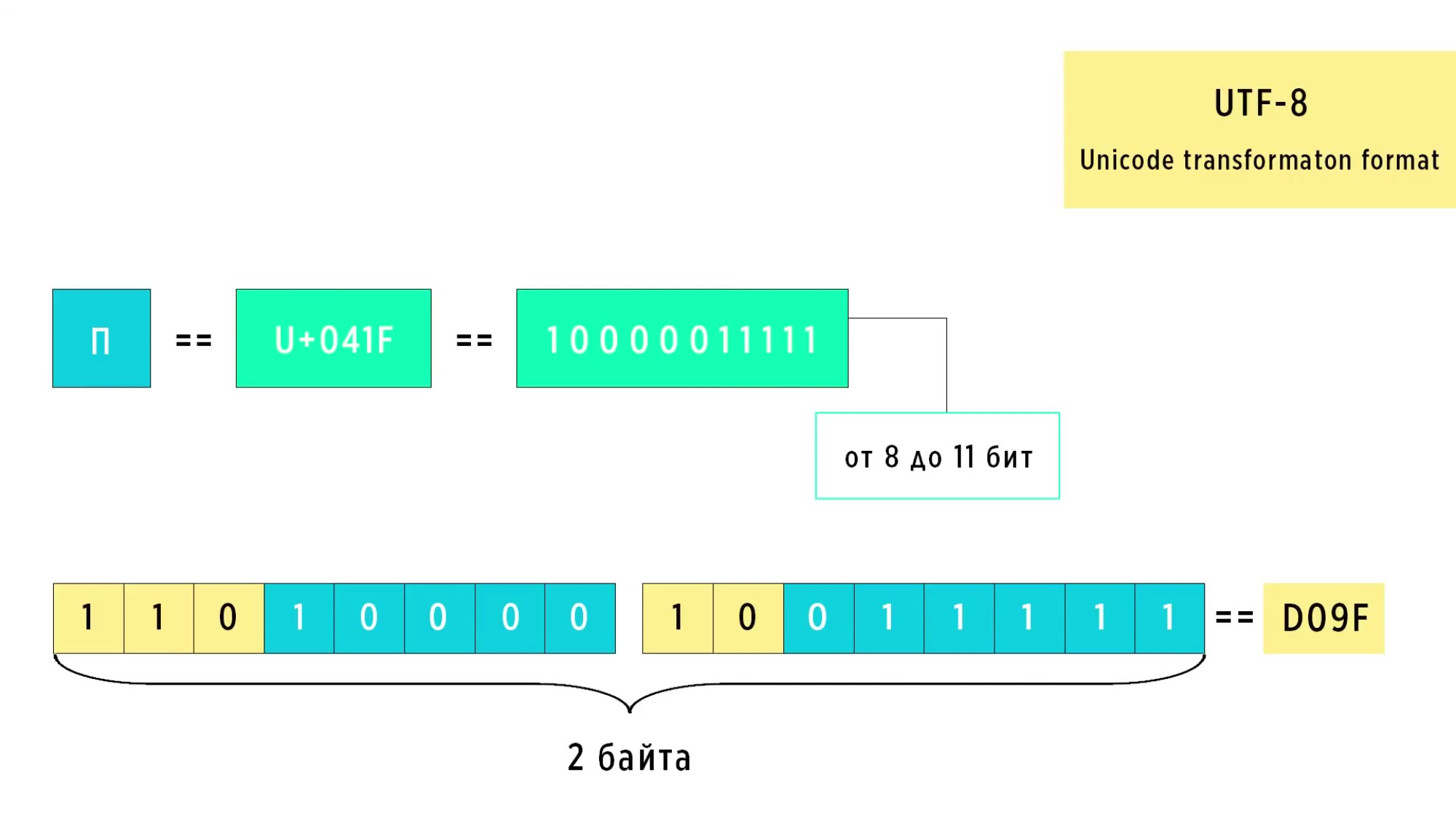
Продолжаем. В Юникоде буква П обозначена кодом 041F. Переведя его в двоичный вид, мы получим код длинной 11 бит, то есть 10000011111. Как это делается можно посмотреть Здесь2 .

Для кода длиной в 11 бит используется вторая маска. В начале обоих байтов подставляем метки и заполняем оставшиеся место двоичным кодом символа.

Чем стандарт отличается от кодировки?

Юникод – не кодировка, а стандарт кодирования, кодировки – это UTF-8, UTF-16 и так далее. Любой символ по этому стандарту имеет свой код и формат записи этого кода. О формате записи говорилось выше. Чем стандарт отличается от кодировки? Понимаю я это так, что кодировка не создаёт новый код для буквы П. Каждая кодировка изменяет, преобразует уже существующий код символа по своему закону, чтобы хранить в памяти устройства, передавать между устройствами и прочее.

Итак, на рисунке мы получили 2 байта, в которых записано 1101000010011111. Чтобы получить букву П в кодировке UTF-8 нужно перевести код 1101000010011111 обратно в шестнадцатеричный формат. Как это сделать можно посмотреть Здесь3 .

Переведя этот код обратно в 16-теричный формат, мы получаем D09F и в таблице кодов UTF-8, мы можем найти требуемый символ. Это будет наша буква П. Полная таблица кодов UTF-8 велика. Её можно посмотреть в интернете. Далее, приведена небольшая её часть:

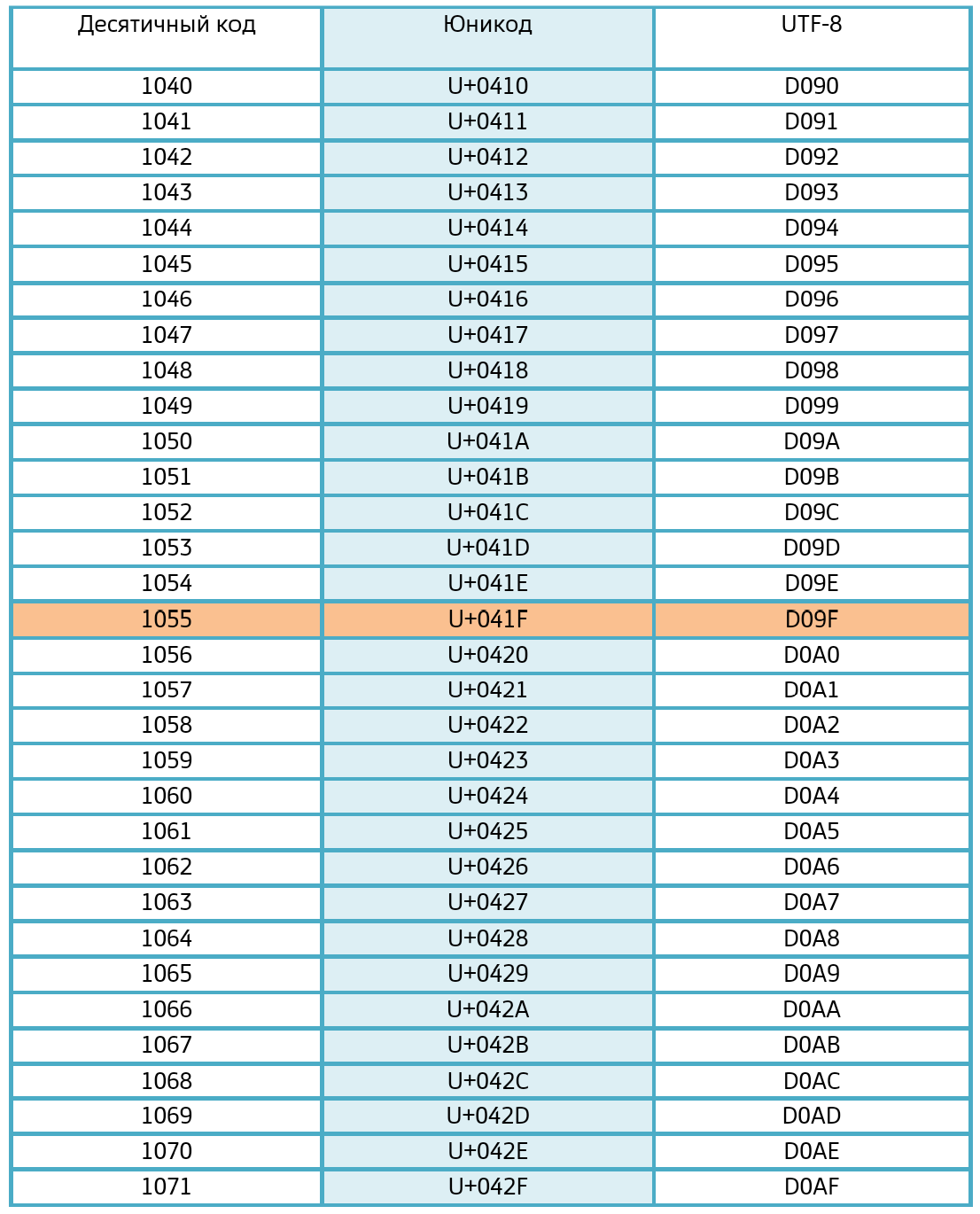
Сколько символов Юникода можно разместить в кодировке UTF-8 ?

Ответ: все. В Юникоде около 150 000 символов. Об этом говорилось выше. В UTF-8 максимальное количество символов, которое можно закодировать, составляет 1 112 064. В шестнадцатеричной системе счисления, применяемой в UTF-8, каждый символ представляется двумя шестнадцатеричными цифрами (от 00 до FF). Количество шестнадцатеричных цифр, используемых для кодирования символа UTF-8 зависит от диапазона Юникода.

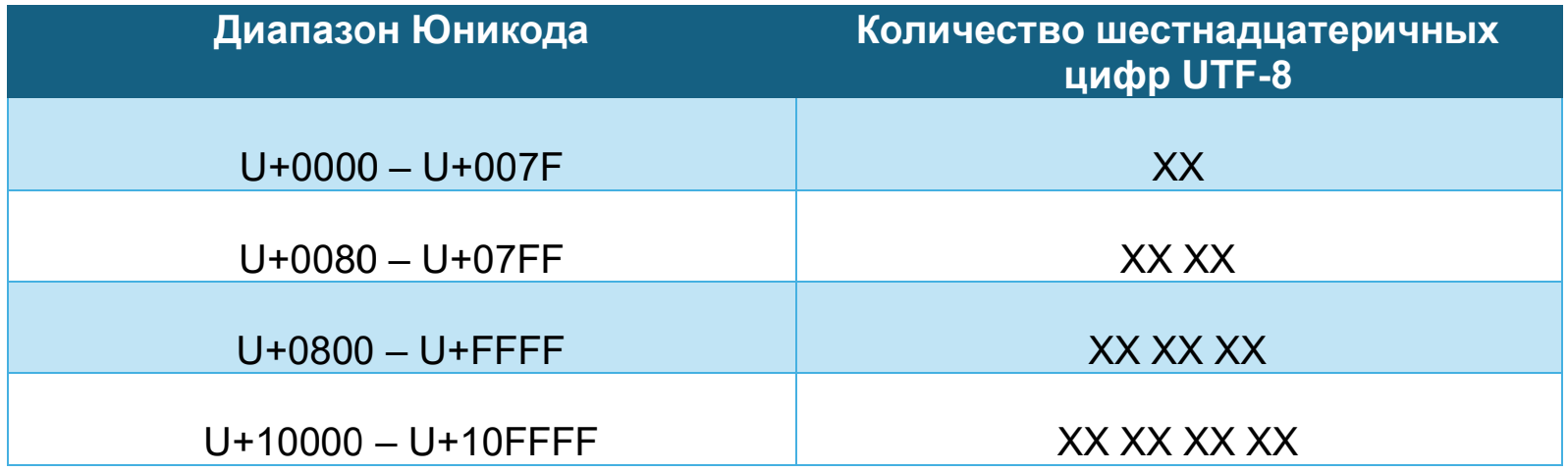
Если посмотреть в конец полной таблицы Юникода, то Unicode имеет максимальную кодовую точку U+10FFFF, то есть кодирует свои символы от 0000 до 10FFFF.

Казалось, что UTF-8 окончательно решил все проблемы, но его нововведение, в виде динамического размера символов, привело к увеличению времени обработки строк. Каждый символ нужно было проверять на его длину и таким образом, код стал работать медленнее. Из-за этой медлительности, многие языки программирования продолжали пользоваться старой кодировкой UCS-2, где на каждый символ приходилось по 2 байтов. Применялись другие старые способы кодирования.

UTF-16.

Как не странно, через небольшое время оказалось, что этих 2 байт старых кодировок не хватает для хранение всех требуемых символов. Поэтому развитие кодировок продолжилось и на свет появился UTF-16. В требованиях к новой кодировки была возможность хранить более чем 2 байта и чтобы при этом оставалось совместимость со старым кодом, написанным с использованием старой кодировки. UTF-16 справился с этими требованиями и обратная совместимость достигалась благодаря тому, что символы от 0 до 2¹⁶ степени (65536) представлялись идентично кодировки UCS-2. Для их хранения также использовались 2 байта, поэтому старые программы, написанные в старой кодировке, могли работать в новой.

Число 16 в названий как раз говорит о том, что минимальная длина символов в этой кодировке 16 бит. Новые же символы, чьи коды выходят за пределы 2 байт, хранятся используя 4 байта памяти.

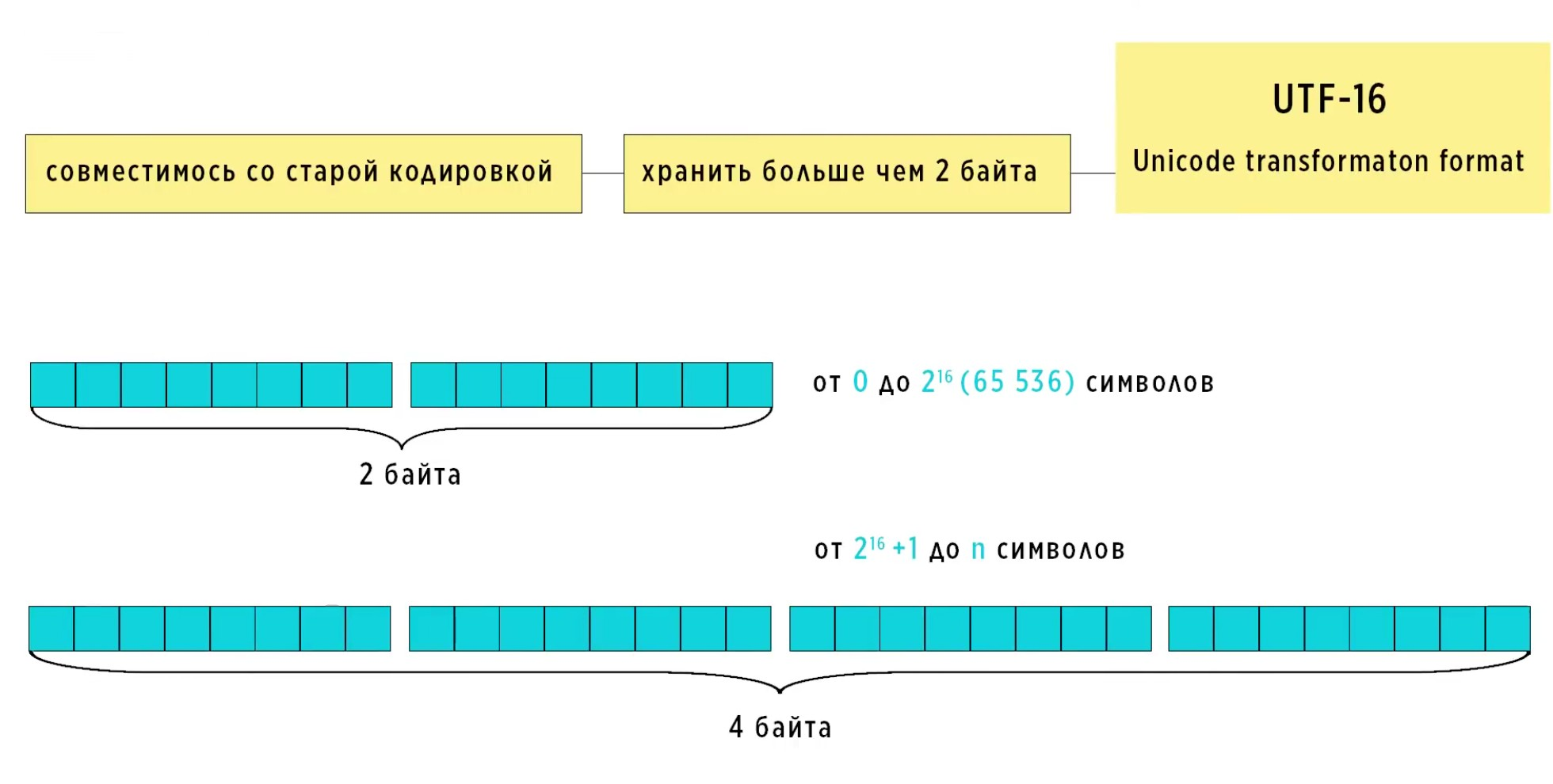
Такой способ хранения стал называться суррогатной парой. Алгоритм кодирования заключается в следующем. Коды символов, которые будут храниться используя 4 байта, находятся в диапазоне таких вот чисел в 16-тиричной системе счисления. Все коды Юникода, которые меньше 10 тысяч, хранятся используя 2 байта, но в этом 2 байтовом диапазоне есть диапазон неиспользуемых кодов. Начинаю от D800 по DFFF, то есть коды из этого диапазона не используются для кодирования символов. Эта область отведена специально для кодирования суррогатных пар. Для примера рассмотрим один из таких символов из Юникода (U+10459, относится к 10000 и выше) для хранения которого изначально требуется 3 байта. Из кода этого символа вычитается 10 тысяч, опять же в 16-тиричной системе счисления. Обратите внимание, в шестнадцатеричной системе.

Для 10459:
10459 – 10000 = 459
Для 104FB:
104FB – 10000 = 4FB
Как вычитать в шестнадцатеричной системе можно посмотреть Здесь4 .

Продолжаем для символа U+10459. После вычитания, мы получаем число 459. Переводим 459 в двоичный вид. Получим 10001011001, длинна которого будет находиться в диапазоне 0 до 16 бит.

Лидирующие 5 нулей не меняют числа. Нам нужно иметь 16 бит. К получившемуся числу в старшие биты, приписываем ещё 0, чтобы получилась длинна в 20 бит.

Далее, разбиваем это число на 2 части, по 10 бит. К старшей половине прибавляем D800. K младше половине прибавляем DC00. Оба этих числа взяты из диапазона для кодирования суррогатов.

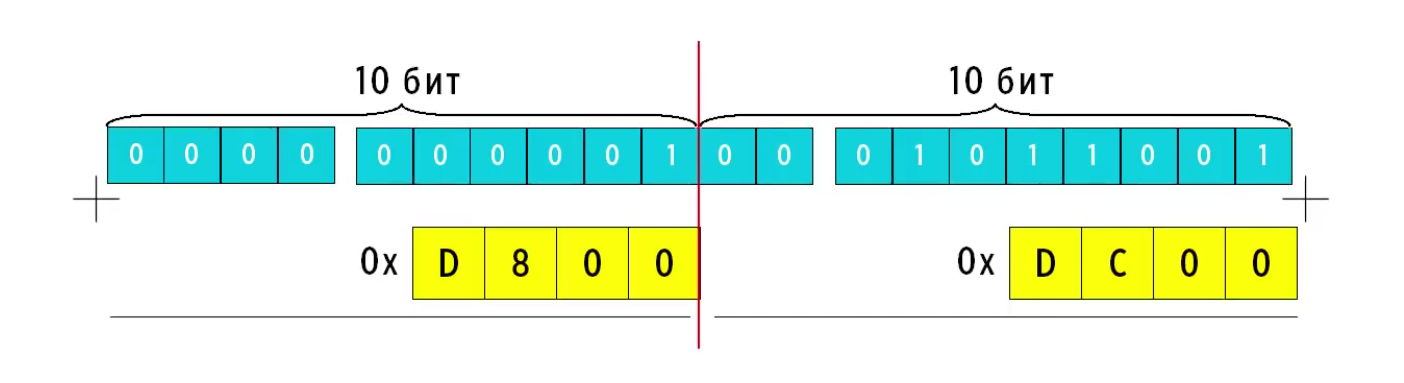
Разбиваем 20 бит, 2 части по 10 бит, UTF-16.

Что такое 0x на рисунке перед D800 и 0x перед DC00?

В шестнадцатеричной системе числа обычно записываются с префиксом "0x" для обозначения системы счисления. Таким образом, наши числа будет иметь вид 0xD800 и 0xDC00, где x – английская буква x.

Итак, к одному числу надо прибавить другое. Для этого предварительно переведём D800 и DC00 в двоичный вид.
D800 / 1101100000000000
DC00 / 1101110000000000
Прибавим.
0000000001 + 1101100000000000 = 1101100000000001
0001011001 + 1101110000000000 = 1101110001011001
Как сложить 2 двоичных числа можно посмотреть Здесь5 .

Мы получили 2 двухбайтовых числа.

Первое число будет находиться в диапазоне D800 до DBFF. Второе от DC00 до DFFF. В итоге склеив эти 2 числа, мы получаем такой вот четырехбайтовое число: 11011000000000011101110001011001. Переводим это двоичное четырехбайтовое число в шестнадцатеричный вид. Посмотреть можно Здесь6 . Получится для символа из Юникода (U+10459) код этого символа, представленный в кодировке UTF-16 будет D801DC59.

Если при чтении этого символа из памяти встречаются символы из неиспользуемого диапазона, значит символ закодирован в суррогатном виде и значит нужно вычитать из памяти четыре байта. Если таких символов нет, значит читаем 2 байта. Поскольку каждый код символа вновь задавался четным количеством байт, то по-прежнему необходимо было использовать BOM-байты для определения порядка хранения символов в памяти. Хоть UTF-16 стал занимать больше места, но работает он быстрее чем UTF-8, поскольку не нужно определять длину строки, не нужно ходить по памяти и искать начало символа. Мы всегда читаем символы до 216 по два байта (2 байта = 16 бит = 216 = 65536 значений) и это работать намного быстрее. Поэтому, UTF-16 стал использоваться во многих языках программирования, таких как Java, C# (произносится си шарп), Java Script и так далее.

UTF-32.

Однако, придумали еще одну кодировку UTF-32. Проблема UTF-16 была в том, что символы за пределами 216 байт требуют для хранения 4 байта. В языках начали использоваться символы, которые выходят за пределы 2 байт и следовательно их нужно было бы кодировать в суррогатном виде. Это в свою очередь увеличивает время обработки строк. В UTF-32 сделали фиксированный размер кодов 4 байта, что позволило быстро разбивать строки по символам, двигаясь в памяти всегда по 4 байта вперед. Скорость чтения кода возрастает. UTF-32 используется в некоторых языках программирования, например, в Питоне. Число 32 в названий говорит о том, что длина символа в этой кодировке 32 бита.

В шестнадцатеричной UTF-32 используются BOM-байты?

В шестнадцатеричной UTF-32, как правило, не используются BOM-байты (Byte Order Mark). Вот почему:
⦁ Порядок байтов: UTF-32 всегда предполагает большой порядок байтов (Big Endian), где старший байт кода символа находится в младшем адресе памяти. Это означает, что порядок байтов в файле с кодировкой UTF-32 всегда одинаковый, независимо от платформы.
⦁ Отсутствие неоднозначности: В UTF-32 нет необходимости в BOM для определения порядка байтов, так как он всегда неизменен. BOM в этом случае был бы излишним.
⦁ Стандарт: Стандарт Unicode не требует использования BOM в UTF-32.

Однако, в некоторых случаях BOM всё же может быть добавлен в UTF-32 файл:
⦁ Совместимость с другими кодировками: Некоторые программы могут использовать BOM для определения кодировки файла, даже если она изначально предполагается как UTF-32.
⦁ Дополнительная информация: BOM может служить в качестве дополнительной информации о файле, например, о его создателе или версии.

В целом, можно сказать, что BOM в UTF-32 не является обязательным, и его наличие или отсутствие не влияет на корректность кодировки. Однако, следует учитывать, что некоторые программы могут ожидать его наличия и неправильно обрабатывать файл без BOM. Важно отметить: Если вы собираетесь работать с файлами UTF-32, необходимо убедиться, что ваша программа не зависит от наличия BOM.

Рассмотрим пример для символа Юникода U+10459.

Как преобразовать U+10459 в шестнадцатеричный UTF-32?

Для преобразования нужно учитывать следующее:
1. Unicode-код уже является шестнадцатеричным представлением. U+10459 – это просто запись Unicode-кода в шестнадцатеричном формате.
2. UTF-32 – это просто способ кодирования Unicode-кодов. В UTF-32 каждый символ кодируется 4 байтами.
3. Шестнадцатеричное представление Unicode-кода U+10459 в UTF-32 будет выглядеть как 00010459, то есть просто добавить впереди нули до 8 знаков.

Объяснение.
⦁ 000: Эти три нуля – заполнение для достижения полного 4-байтового представления, свойственного UTF-32.
⦁ 10459: Это собственно шестнадцатеричный код символа U+10459.
Таким образом, шестнадцатеричное представление Unicode-кода U+10459 в UTF-32 – это 00010459.

Для наглядности приведена небольшая часть таблицы UTF-32. Полная таблица UTF- 32 велика и содержит код UTF-32 для каждого символа Юникода.

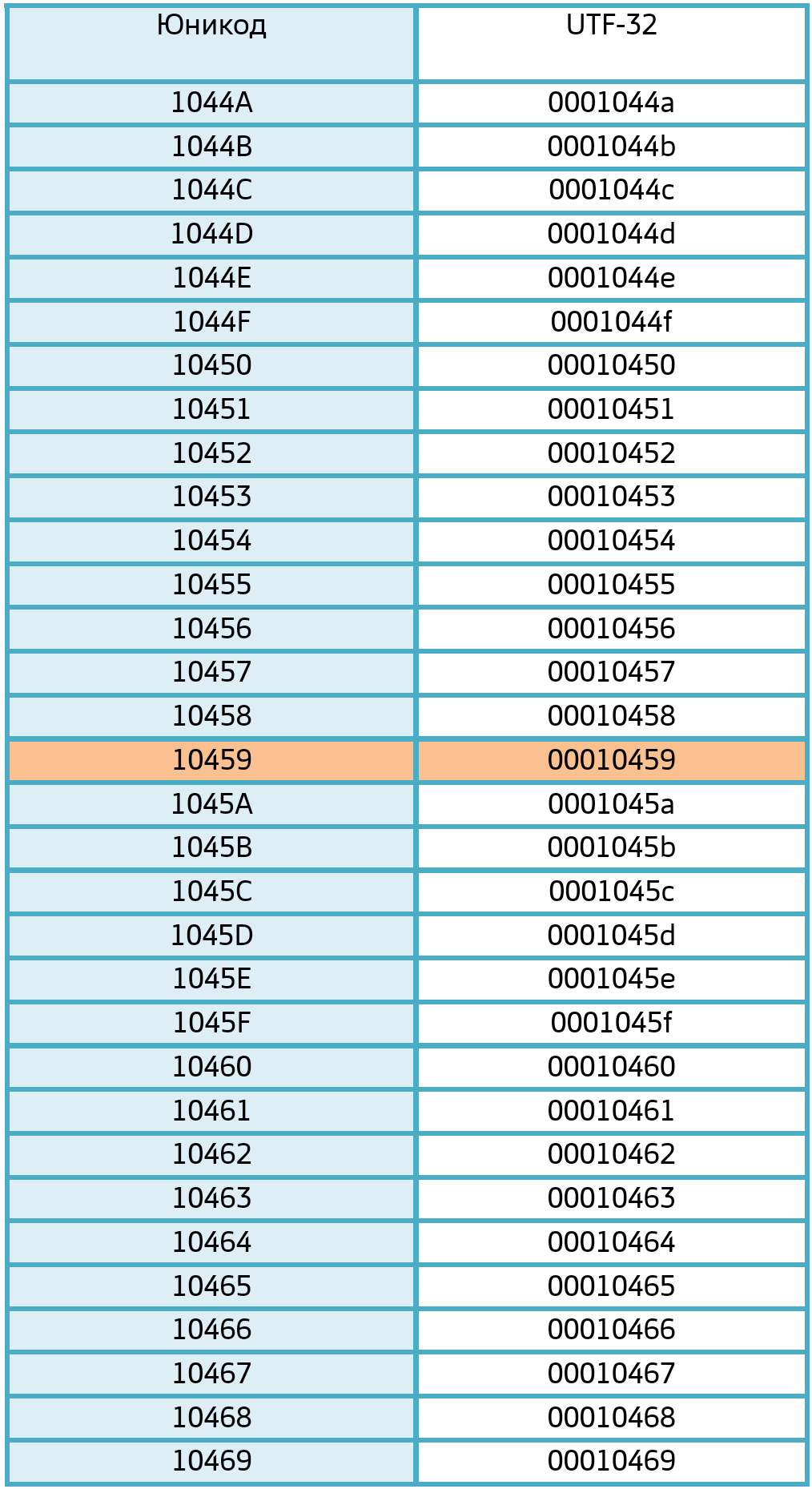
Как преобразовать шестнадцатеричный UTF-32 в двоичный UTF-32?

Для человека удобна таблица и шестнадцатеричная запись UTF-32. Для компьютера нужна двоичная запись UTF-32. Как её получить можно посмотреть Здесь7.

Итак, по ссылке был преобразован шестнадцатеричный код 00010459 в двоичный код 10000010001011001, но это ещё не всё. Это ещё не двоичная кодировка UTF-32. Должны быть заполнены все биты в 4 байтах, то есть 32 клетки на рисунке.

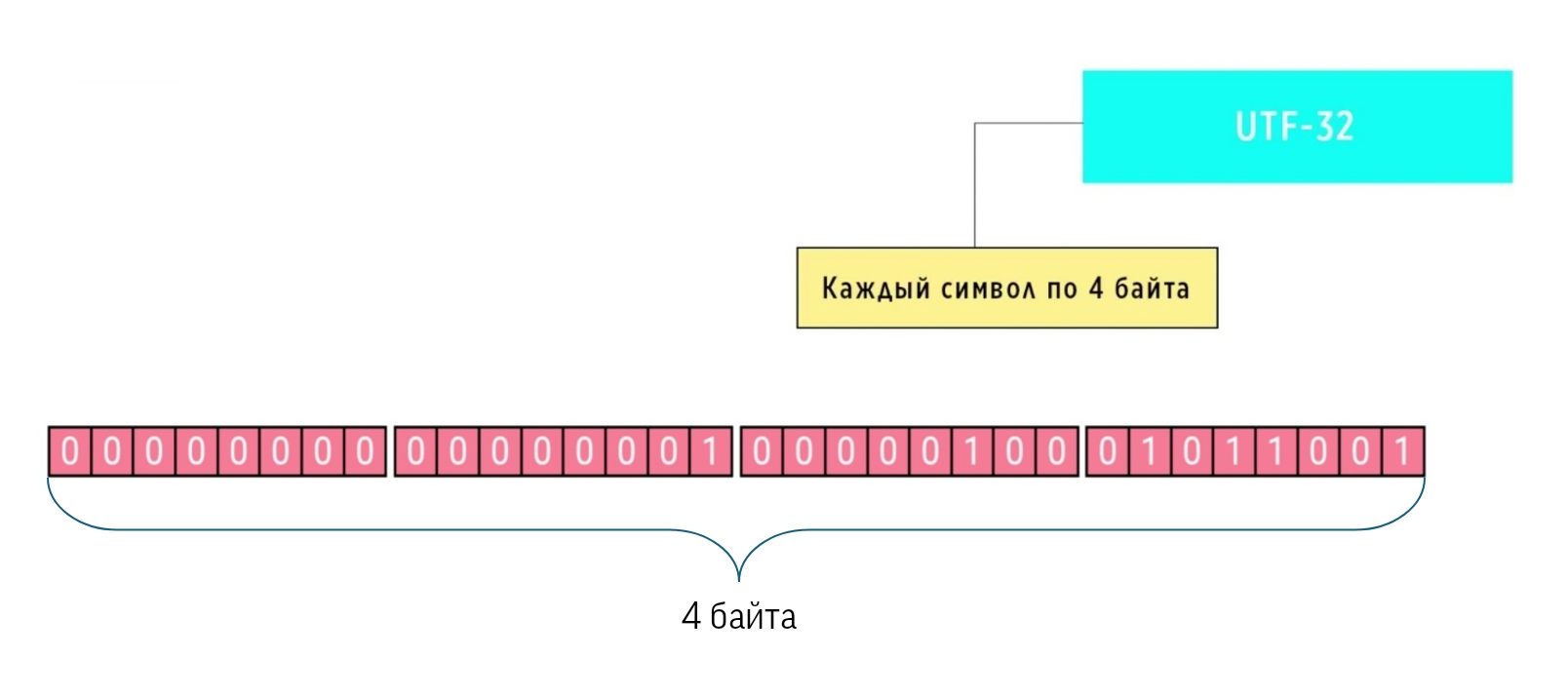
В правые 17 бит записываем 10000010001011001. В левые 15 бит добавляем нули. Получили двоичную кодировку UTF-32. Много "лишних" нулей? Такая кодировка. Пример был для символа U+10459, который находится где-то в середине Юникода. Если двигаться в конец таблицы Юникода, то количество нулей будет уменьшаться. Если двигаться в начало, то увеличиваться.

Каждая кодировка подходит для своих задач. Например, файлы кодировки UTF-8 занимают в 4 раза меньше места чем кодировки UTF-32, поэтому UTF-8 используется для передачи файлов по интернету. UTF-16 и UTF-32 работают быстрее, поэтому используются в языках программирования. Создать что-то универсальный не удалось, поэтому используем все это наследие, которое нам досталось.

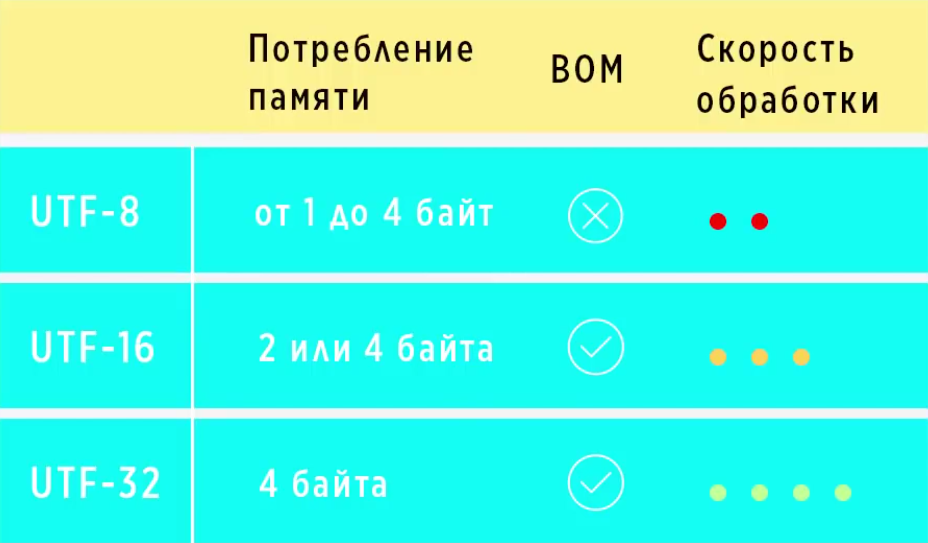
Таблица сравнения, потребление памяти, BOM, скорость обработки.

Работая с кодом, нужно всегда обращать внимание, в какой кодировке вы это делаете, чтобы не получить непонятные знаки вместо нормальных символов, которые там должны были быть. Непонятные появляются тогда, когда мы используем символы, которых нет в используемой кодировке или открываем файл программой, которая не поддерживает нужную кодировку.